Hand Force and Swimming Velocity
Rod Havriluk, Ph.D.
XVth Federation Internationale de Natation World Congress
Indianapolis, IN, 2004
The relationship between force and velocity in swimming has been investigated under both passive and active conditions. The most basic form of the equation is expressed as: D = kvn, where D is the drag force on the body; k includes the coefficient of drag and an area variable; and v is the swimming velocity raised to an exponent of n.
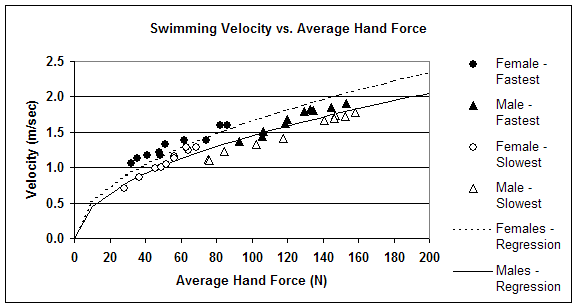
A recently conducted meta-analysis on passive drag confirmed the quadratic relationship between resistance and velocity (Havriluk, 2004). If the resistance increases quadratically with velocity, then propulsion must increase in the same manner. The purpose of this study was to determine the relationship of hand force and swimming velocity. It was hypothesized that there would be a quadratic relationship between force and velocity.
The results support the hypothesis that there is a quadratic relationship between force and velocity in swimming. The within subjects design shows that a swimmer will swim faster with an increase in hand force. The between subjects design shows that swimmers who exert more hand force swim faster than swimmers who exert less hand force. Any differences in the k values for the within and between designs can be attributed to the components of k: cross-sectional area of the body and drag coefficient.
Understanding this relationship is paramount to optimizing performance. Since a disproportionately larger increase in hand force is required to continue to increase swimming velocity, swimmers must be very conscious of generating maximum force and optimally directing the force at the higher swimming velocities.
This information is critical to coaches and can be used in many ways. In the most obvious approach coaches can encourage swimmers to exert maximum hand force throughout the entire stroke and to maintain high force values throughout a training session. In a more refined approach that usually requires quantitative feedback they can adjust bilateral differences and minimize force losses and wasted motion.